In this second part of the article series ‘Understanding Strong Materials’ we will explore physical design strategies to optimise the strength of products you design. Sometimes we need to make compromises between strength and weight to strike a balance that is fit for purpose. Reading the first article will be helpful understanding certain material properties so this should be considered assumed knowledge. Please comment!

Article by Martin Gibson – Twitter – 26.02.2010

Why Do We Need Strength?

Since the conception of consumerism designers have been on a quest to make everyday products stronger for a variety of reasons. Whether it is to make a product last longer than previously conceived, to make a product safer and more durable or as a marketing angle to persuade consumers to upgrade, product strength is invaluable to the design profession.

On the other end of the spectrum there are designers who quest to make products the bare minimum strength. That is, they may want to make their products to use the minimum amount of materials to save money, save weight, and to save materials (you know the sustainable design movement you hear too much about).

No matter what designer you are, understanding how to get the most out of your materials strength-wise is an excellent transferable skill across any industrial design discipline.

Design Strategies

Use Smart Shapes

The most effective way to design strength into your products is by using strong shapes and forms. After thousands of years of architecture and civil engineering we have learnt that some shapes are inherently stronger than others.

However certain shapes are stronger than others in different contexts. For example when constructing a building utilising vertical columns and right angled ceilings is the most logical shape as the beams best support the downward gravitational force. When designing a shape to resist impact force triangles are a great shape as no matter what side gets impacted the shape has a reactive resistance (not to mention circles and arches).

This rudimentary assessment of 2 dimensional shape strength is quite self explanatory. However when we get into complex 3d forms and mouldings these simple rules can get thrown out of the window. LaPlace’s Law states that double the curvature of a shape gives greater strength and stiffness for any given material. Therefore arches, spheres and hemi-spheres become inpenetrable objects. Hence why we see arch bridges, and why coconuts take a large amount of force to break despite their light weight.

But as mentioned before a strong shape depends entirely on its context. All these arches and domes are great building shapes but they are terrible at withstanding localised loads, but when well-braced they can have a transmural-effect to distributing energy.

Extrusions, particularly circular and oval shaped, can also be sufficiently strong for any human purpose when constructed out of metal alloys, as once again these shapes are ‘load sharing’ shapes. Have you ever held a metal circular extrusion in your hand and hit it against a solid surface? You will notice the whole piece of metal will vibrate vigorously as the force is distributed uniformly.

If strength is absolutely critical to your product you can also consider combining these shapes together. For example an extrusion with a cross section of a triangle with an internal circle becomes incredibly strong.

Use the Correct Materials

When designing a product to optimise strength one must take a real holistic approach to the design process. That is, when designing the shape of your product in the back of your mind you must be thinking about what material the product should be made out of (as one knows not every material can be manipulated into every shape, and some materials act differently due to grain and density when in different states). This dualistic process of design can be difficult to grasp and might force you to look at other products on the market as a starting point. However don’t settle for what materials are utilized in the present market, we have seen time and time again new materials transforming market sectors, so be creative.

I am going to refrain from explicit detail here as material usage in different industries can vary drastically. But to give you a general overview metals both pure and alloy can be great when high strength is required, but they tend to be quite heavy. Metal tends to come in sheets or extrusions but can also be moulded. Likewise plastic is another mouldable material, and although generally not as strong as metals it can be great for domestic and mass production means. There is also the traditional wood materials which also tend to be strong but not as strong as metal, but stronger than plastic.

There are also composites, glass, cards, rubbers and fabrics which can also take on a variety of forms. But always remember to keep in the back of your mind that materials have different prices, availability, manufacturing and fabrication requirements which must all be entailed in your decision making process.

Use the Right Thickness

Materials come in a variety of thicknesses and for designers concerned about the environmental impacts of material usage or need their product to weigh the absolute minimum, study of wall thicknesses is essential. For mouldable plastic products manipulating the thickness of wall thicknesses can be very easy through CAD modelling. And although these programs contain increasingly sophisticated force analysis simulations, still in a professional product development environment the formation of the optimal wall thickness is still very much a trial and error process. That is, the production of many prototypes is required, each with varying wall thicknesses and user trials are then conducted to test their yield strength. Ultimately we must appreciate that products we design can be used not as protocol and user studies will always be the undeniable truth as to your products real strength.

Use the Right Fasteners

Choosing the right fasteners and fittings for your product is essential to optimising your products durability. Ideally you want fasteners that are stronger than the present standard material. Often when fasteners are used as joints, it is often the fastener that must withstand the majority of the force. Not only should the fasteners or joints themselves be cleverly constructed but they must be fastened onto the existing material in a secure manner.

Calculating Force

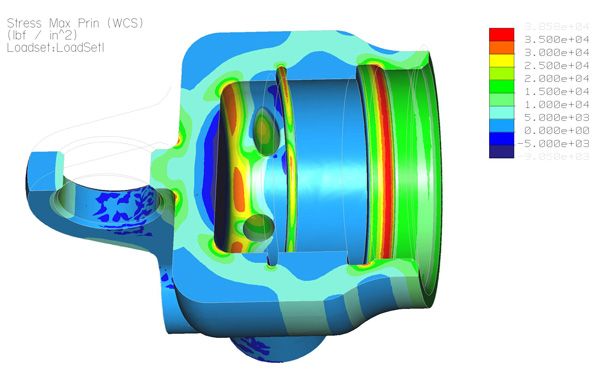
Calculating force on your product can be a daunting task especially if there are multiple forces, multiple force types (constant, variable, localised, global etc.), multiple joints and material types. But once again remember that no product goes to market without prototypes being constructed, but having good mathematical knowledge can ensure better accuracy of your prototypes. Programs like Solidworks have great in-built simulation and testing features so I recommend checking these out, but they can be processor rigorous and might take professional training to get used to them.

Before you rush in and do a full analysis study, firstly you must do a risk assessment of your product. This involves identifying the weak points of your product and then prioritising these weaknesses so you spend the greatest amount of time and resources on these areas. One must remember though that every weakness should be identified and it’s breakage risk mitigated, as a product is only as strong as its weakest link.

Below we are going to run over a simple but a great place to start when analysing forces on your product. Most of the time the force exerted on your product will be a human force so we must quantify this to begin with. Lets say for example we need to assess whether a human standing on an aluminium platform can be supported without the aluminium sheet bending or snapping. Lets say that the human weighs 75KG. So we must calculate what this force is, therefore we must use the formula:

F=MxA

(F=force, M=mass, A=acceleration)

Therefore,

Force= 75KG x 9.8m/s

(the 9.8m/s is the constant gravitational acceleration of the earths atmosphere)

Therefore,

Force= 75 x 9.8= 735 newtons force

Now back to that aluminium platform. Lets say that the humans shoe (the area of impact on the platform) is 0.1m x 0.2m. This gives us an area of 0.02m(2) (we must multiply this by two as the person is going to have two feet on the platform) which results in 0.04m(2). Now we have all the data required to calculate the pressure on the aluminium platform. We can use this formula:

P=F/A

(P=pressure, F=force, A=area)

Therefore,

P= 735 netwons / 0.04m(2) = 18 375 Pa or 183MPa

Now if go to MatWeb www.matweb.com we could then search for materials that can withstand that kind of tensile strength yield and tensile strength ultimate pressure. In this case the piece of aluminium has a tensile strength ultimate of 310MPa, and yield of 276 MPa so it theoretically could support this human weight. But of course the calculation can get a lot more complex. For example, what if we changed the shape of the platform so that it was smaller or larger, or if we put supporting beams underneath the platform, or if we made the platform material thicker?